Dopo il grande interesse per le attività che vi ho proposto nel precedente articolo (adatte principalmente alle prime classi della scuola primaria), vi mostro come i mathlink cubes possano essere utilizzati anche nelle classi più grandi.
Conosci i Matklink cubes? Si tratta di cubetti ad incastro di cui esistono alcune versioni diverse per tipologia e materiale:
- i classici Mathlink Cubes in plastica con connettori un po’ più grandi;
- i Fidget Cubes, sempre in plastica, un po’ più facili da incastrare e decorati, più adatti ai bimbi più piccini;
- i Cubi ad incastro in legno riciclato in 10 colori, incastrabili in più modalità;
- i Cubi ad incastro in legno riciclato rossi e blu.
Tutte queste versioni sono in confezioni da 100 pezzi e i cubi hanno la dimensione di 2 cm.
Inoltre per le classi più alte esistono anche due varianti di PICCOLE DIMENSIONI: 1 cm x 1 cm x 1 cm che oltre ad essere adatte per le attività che ti suggerirò sono anche molto comode perché possono essere utilizzate per le misurazioni precise (ogni cubetto incastrabile è della dimensione di 1 cm, quindi è facile misurare!) e inoltre hanno il peso di un grammo, quindi possono essere utilizzati addirittura come unità di misura di peso sulle bilance. Super!
Ecco le due versioni piccole:
- i Cubetti ad incastro in plastica riciclata (confezione da 1000 in una pratica scatola di legno);
- i Cubetti ad incastro in plastica (confezione da 1000 in sacchetto).
Questi cubetti sono stati anche utilissimi per i bambini della classe 4C di Cristina che grazie ad essi hanno scoperto un TEOREMA!
Tabelline
Possiamo proporre le tabelline come costruzioni di rettangoli in modo tale che possa risultare evidente la moltiplicazione e il risultato della stessa operazione.

Si possono proporre tutte le tabelline usando questo strumento
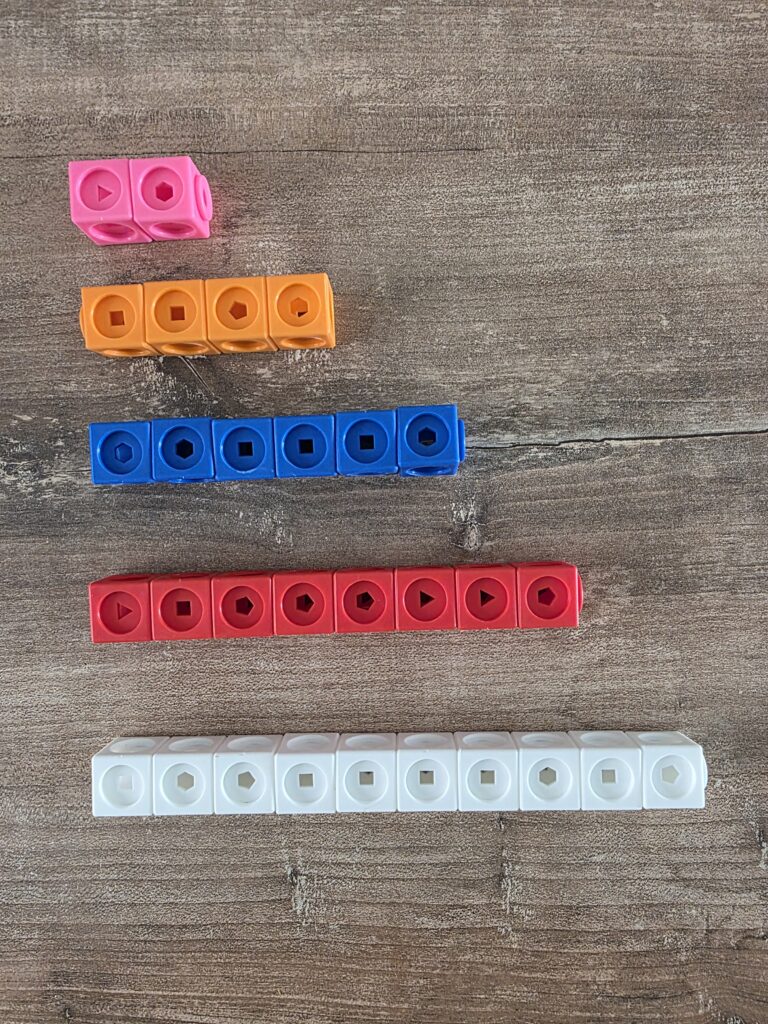
Tabellina del 2
2×1 =2
2×2 = 4
2×3=6
2×4=8
2×5=10
Area del rettangolo e del quadrato
Dopo aver visto la moltiplicazione come diagramma del rettangolo, non sarà difficile fare il passaggio alla misurazione dell’area del rettangolo e del quadrato usando la stessa strategia.

Giocando con le tabelline e con il calcolo dell’area, è possibile far notare ai bambini anche i numeri quadrati e i numeri rettangolari.

9=3×3 è un numero quadrato
10=5×2 è un numero rettangolare
Per il calcolo del perimetro bisogna prestare un po’ più d’attenzione dal momento che i bambini potrebbero essere tratti in inganno dal numero di cubetti (invece di contare i lati del cubetto). Valutate voi se può esservi utile per parlare di perimetro altrimenti utilizzate altri materiali.
Divisioni
Questo strumento può essere anche utile per un primo approccio alle divisioni.
I bambini, data una divisione, possono raggruppare, ripartire, distribuire toccando con mano l’operazione.


Simmetrie
Possiamo poi chiedere ai bambini di osservare e creare costruzioni simmetriche (verificando grazie ad uno specchio la correttezza o meno della proposta).
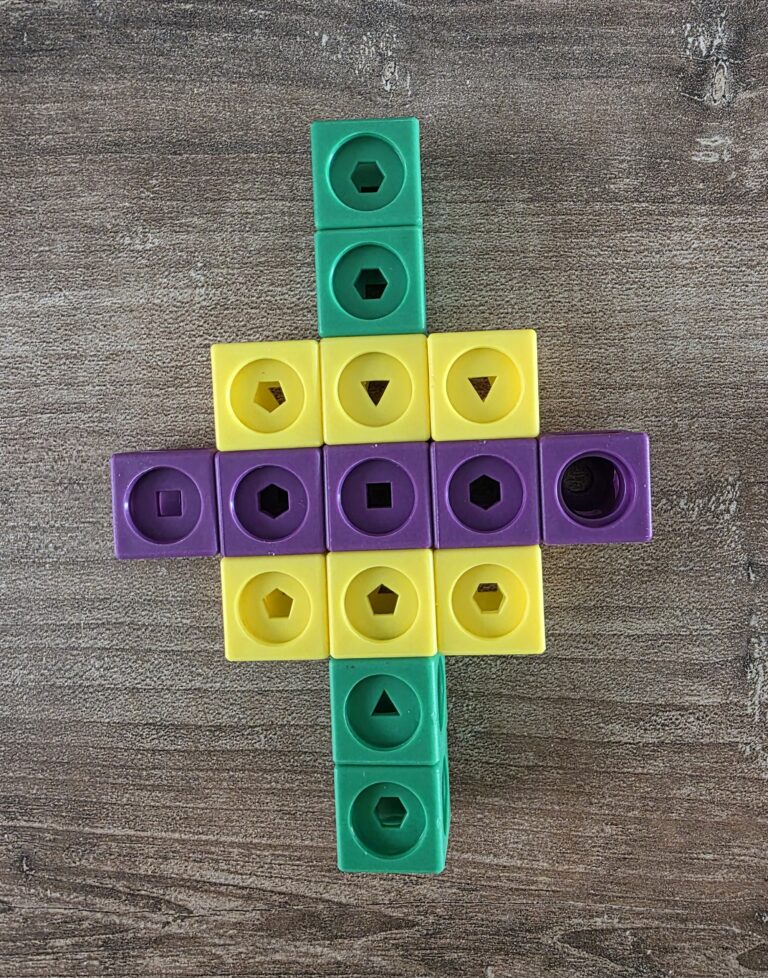
Una variante può essere quella di fornire agli alunni una costruzione e chiedere loro di creare l’esatta simmetria o ancora fare soltanto metà disegno e i bambini dovranno terminarlo rispettando la simmetria.
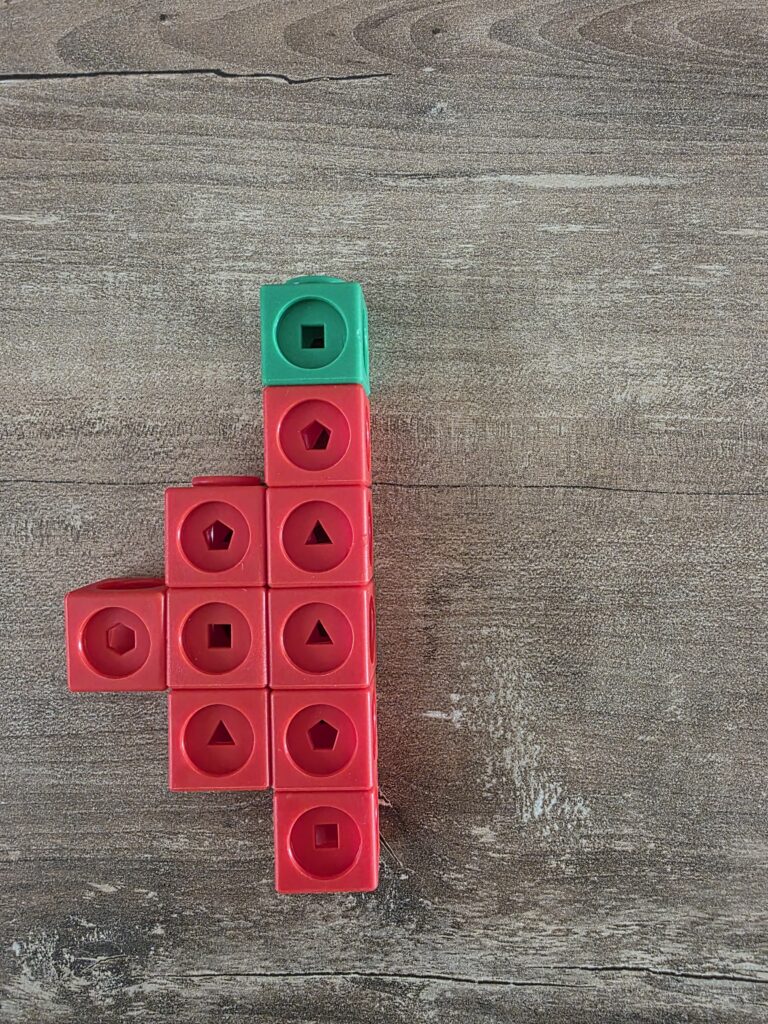
Quest’attività può essere fatta a tu per tu insegnante-alunno o mettendo gli alunni a coppie e chiedendo loro di sfidarsi: il primo propone un’immagine e il secondo realizza la simmetria, poi si invertono.
Volume e punti di vista
Si può chiedere ai bambini di creare delle costruzioni tridimensionali per poi passare a domandare loro qual è il volume espresso in cubetti (quanto spazio occupano?).

Per le classi più grandi si può passare poi a parlare di punti di vista e chiedere quindi agli alunni di disegnare sul quaderno questa costruzione vista dall’alto, poi da davanti, da un lato e così via.
La presenza del materiale può permettere agli alunni di verificare l’ipotesi rappresentata sul quaderno o essere di supporto nella realizzazione per gli alunni più in difficoltà.

In allegato potrete scaricare due tipologie di carte a partire dalle quali è possibile fare una serie di attività.
-Per prima cosa i bambini possono semplicemente riprodurre la costruzione che vedono
-In un secondo momento possiamo chiedere loro di disegnare sul quaderno come la vedono dall’alto, da davanti,… facendo così un lavoro sui punti di vista.


Utilizzando invece queste altre carte, possiamo far giocare i bambini a coppie: il primo ne sceglie una senza dirlo al compagno e riproduce l’immagine che vede, il secondo, osservando la costruzione, dovrà capire qual è la carta corretta.
Per rendere il gioco più difficile, il compagno potrà ruotare la costruzione, camuffando il prodotto finale.


Attività simili si trovano anche sui libri La Matematica con il Cubo Soma, associati ai pezzi di questo curioso strumento, ma che possono essere facilmente riprodotti attraverso i Mathlink Cubes.
Pixel Art e Coding
I cubetti tornano anche molto utili quando realizziamo disegni con la pixel art per trasformare il prodotto in qualcosa di tridimensionale: quindi i bambini potranno seguire un codice scritto e realizzare il disegno prima con i cubetti poi sul foglio.

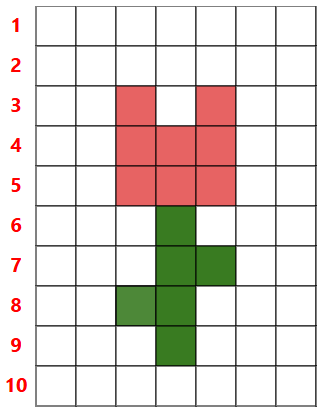
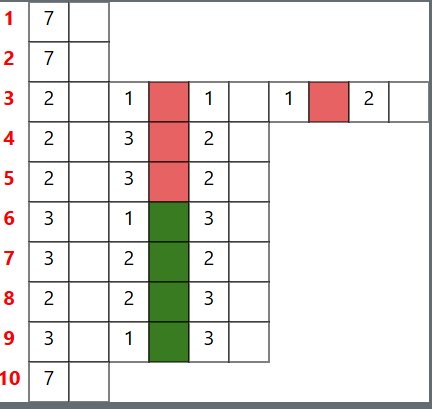
Come variante si può anche proporre ai bambini di estrapolare il codice direttamente dal disegno e proporlo ai compagni e alle compagne.









1 Comment
Grazie infinite, ottimi suggerimenti pratici e accattivanti.